引言

布雷斯悖论来自于一个真实的现象：城市的某个繁华路段特别的堵塞，人们在其边上新修一条道路，期望舒缓整个交通网路的堵塞状况。

道路刚修好时特别令人兴奋，但很快，新修的道路也被严重堵塞了，而更令人困惑的是：原先堵塞的路网似乎并未从新修道路的分流中得到好处，也比之前更堵了。

用更学术语言来表达就是：当在一个繁忙交通网上增加一条交通线路，新增线路不但没有减少原有的交通延滞，反而拉低了整个交通网络的服务水准(level ofservice)。这种现象与人类的常识相悖，被称为布雷斯悖论。

描述

如果觉得不可思议，不妨看一下这个概念模型。

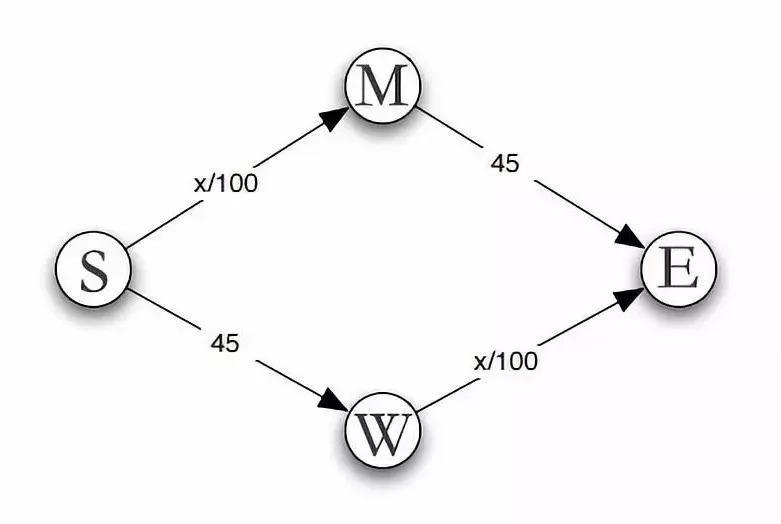
每天都有一批人必须从S点前往E点。

而想要完成这段路程，共有2条线路，分别为SME或SWE。

其中SW与ME的路况较好，无论有多少车辆驶过都只需要45分钟。

但SM段与WE段就不同了，比较容易堵车：随着车流量x的增大，所需时长（x/100）也会增加。

现在假设每天都会有4000辆小汽车会从起点S前往终点E。

这时，一场博弈已经展开了，站在分叉路口上的老司机会选择走哪条路呢？

如果有a人选择走SME路线，那么总时长则为a/100+45，而走另一条路SWE的总时长则为45+（4000-a）/100。

由此可见，无论哪条路人更多，该路段的通行时间就会越长。

当然，司机们一开始也无法得知其他人会如何选择路线，便会偏向于随机选择一边。

司马亿每天上班，也同样要经历这样的抉择。

但到后来，如果SME所花时间多，大家便会涌向SWE。

而SWE的人多了所花时间变长了，人们又会自然回到SME。

最终，这两条路都会平均分摊到2000辆的车流量，通行时间固定为2000/100+45=65分钟。

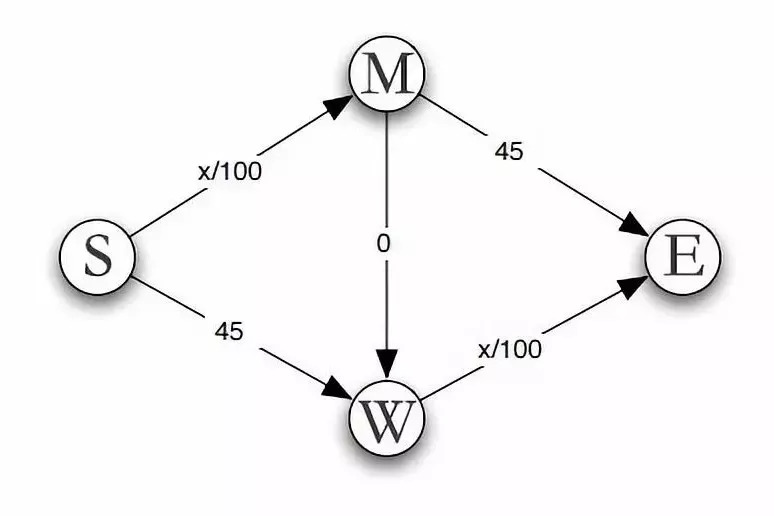
以上，便是修路之前的大致状况了。现在我们就来修路吧，看看会发生什么？

如图所示，在MW之间新增一条快速通道，使得M与W连成一体。

这条路畅通得“如飞一般的感觉”，所花时间几乎可以忽略不计，设为0。

这对全体司机来说，无疑是件大好事。

而且说MW路段是捷径都不为过，他们每一个人都能从这段新路中获得优势。

在这种情况下，就算SM与WE路段挤满了人（即x=4000），这两段路的耗时也只需4000/100=40分钟。

所以相比另外两段路（SW与ME）固定耗时45分钟，走SM与WE路段始终耗时更短。

而我们也注意到，此刻原来两条路线SME与SWE均需要花费85分钟。

经济学中假设每个司机都是自私自利的，他们必然会选择对自己最有益的路线。

于是，所有人会毫不犹豫地选择SMWE这条新路。

用80分钟（4000/100+0+4000/100=80）走完全程。

但是回过头看看才发现，大家都被坑了。

原本在不修这条该死的新路前，无论走哪条路都只需要65分钟。

惊不惊喜，意不意外，多修了一条近路，司机的总通行时长反而增加了。

我们可以注意到，正是“自私”造成了这种困境。

事实上，如果所有司机约定好牺牲一下走回原来的老路，大家都会比现状好些，至少每人都能节省个15分钟。

但在利益面前，人都是趋利的，这也是布雷斯悖论的关键所在。

在这个4000人的博弈中，你个人的选择已经不太重要了，其他的3999人才是重点。

于是我们可以看到，大家都竞相选择最有利的路线。

最后却在无形中之中，使得交通系统崩溃。

布雷斯悖论产生的原因

人这种动物是趋利的，且作为个体身在网络中是无法窥探全局的，因此，其决策都是基于自身利益考虑。新建了一条快速的捷径，于是纷纷走这条路，结果造成了更大的拥堵。

这也是纳什均衡中提到的，个体聪明选择的汇总，其实并非最优解。所以加入了新的道路，反而让所有人都陷入了“囚徒困境”式的纳什均衡。而大家都因忌讳损害自身的利益而选择抄近路，则是布雷斯悖论中的纳什均衡点。

如果我们所有的汽车都是无人驾驶，机器计算，则能迅速计算出最优路线，做出网络效率最大化的决策，避免无谓的拥堵，提高整个城市的生产效率，人类的生产效率又会上升一个台阶。