C++ SKIA绘制过定点的贝塞尔曲线

上星期,为了画出过定点的贝塞尔曲线,纠结了很长时间,最终还是在网上找到了相应的算法,呵呵…

严格意义上来说,这个日志不是我原创的…

谢谢一下两篇日志…

http://blog.csdn.net/microchenhong/article/details/6316332

http://liyiwen.iteye.com/blog/705489

以下代码是skia的绘制代码…

大致思路就是 先算出相邻原始点的中点，在把相邻中点连成的线段，将线段的中点平移到对应的原始点。再以平移后的中点作为控制点，相邻原始点为起始点画贝塞尔曲线，这样就保证了连接处的光滑。而贝塞尔曲线本身是光滑的，所以就把这些原始点用光滑曲线连起来了。

void Draw(SkCanvas *canvas)
{
    SkPoint points[4];
    points[0].fX = 50;
    points[0].fY = 50;
    points[1].fX = 75;
    points[1].fY = 25;
    points[2].fX = 125;
    points[2].fY = 25;
    points[3].fX = 150;
    points[3].fY = 50;
 
    SkPaint p3;
    p3.setColor(SK_ColorBLUE);
    p3.setStyle(SkPaint::kStroke_Style);
 
    SkPath path3;
    path3.moveTo(points[0]);
    path3.cubicTo(points[1], points[2], points[3]);
    canvas->drawPath(path3, p3);
 
    SkPaint p4;
    p4.setColor(SK_ColorRED);
    p4.setStyle(SkPaint::kStroke_Style);
 
    SkPath path4;
    path4.moveTo(points[0]);
    path4.addPoly(points, 4, false);
    canvas->drawPath(path4, p4);
 
    vector<SkPoint> originPt;
    for (int index = 0; index < 4; ++index)
    {
        SkPoint pt;
        pt.fX = points[index].fX;
        pt.fY = points[index].fY;
 
        originPt.push_back(pt);
    }
 
    vector<SkPoint> extrapoints;
    createCurve(originPt, extrapoints);
 
    SkPaint p5;
    p5.setColor(SK_ColorGREEN);
    p5.setStyle(SkPaint::kStroke_Style);
 
    SkPath path5;
    for (int index = 0; index < extrapoints.size(); index += 2)
    {
        path5.moveTo(extrapoints.at(index));
        path5.lineTo(extrapoints.at((index + 1) % extrapoints.size()) );
    }
    canvas->drawPath(path5, p5);
 
    SkPaint p6;
    p6.setColor(SK_ColorYELLOW);
    p6.setStyle(SkPaint::kStroke_Style);
 
    SkPath path6;
    path6.moveTo(originPt.at(0));
    for (size_t index = 0; index < originPt.size() - 1; ++index)
    {
        path6.cubicTo(extrapoints.at(index * 2 + 1), extrapoints.at(index * 2 + 2), originPt.at(index + 1));
    }
    canvas->drawPath(path6, p6);
 
    canvas->save();
    canvas->translate(0, 50);
    SkPaint p7;
    p7.setColor(SK_ColorBLACK);
    p7.setStyle(SkPaint::kStroke_Style);
 
    vector<SkPoint> curvePoint;
    createBezierCurve(originPt, curvePoint);
 
    SkPath path7;
    path7.moveTo(curvePoint.at(0));
    for (size_t index = 1; index < curvePoint.size(); ++index)
    {
        path7.lineTo(curvePoint.at(index));
    }
    canvas->drawPath(path6, p6);
}
 
void createCurve(const vector<SkPoint> &originPoint, vector<SkPoint> &extrapoints)
{
    //控制点收缩系数 ，经调试0.6较好，CvPoint是opencv的，可自行定义结构体(x,y)
    SkScalar scale = 0.6;
    vector<SkPoint> midpoints;
    midpoints.resize(originPoint.size());
    //生成中点
    for(int i = 0 ; i < originPoint.size() ; i++)
    {
        int nexti = (i + 1) % originPoint.size();
        midpoints[i].fX = (originPoint[i].fX + originPoint[nexti].fX) / 2.0;
        midpoints[i].fY = (originPoint[i].fY + originPoint[nexti].fY) / 2.0;
    }
 
    //平移中点
    extrapoints.resize(2 * originPoint.size());
    for(int i = 0 ; i < originPoint.size() ; i++)
    {
        // 求出当前点的前驱和后继
        int nexti = (i + 1) % originPoint.size();
        int backi = (i + originPoint.size() - 1) % originPoint.size();
 
        // 求出当前点的前驱和后继连线的中点
        SkPoint midinmid;
        midinmid.fX = (midpoints[i].fX + midpoints[backi].fX) / 2.0;
        midinmid.fY = (midpoints[i].fY + midpoints[backi].fY) / 2.0;
 
        // 前驱和后继连线的中点移动到当前点的偏移量
        int offsetx = originPoint[i].fX - midinmid.fX;
        int offsety = originPoint[i].fY - midinmid.fY;
 
        // 求出偏移后的前驱和后继坐标(缩放相应的缩放系数)
        int extraindex = 2 * i;
        extrapoints[extraindex].fX = originPoint[i].fX + (midpoints[backi].fX + offsetx - originPoint[i].fX) * scale;
        extrapoints[extraindex].fY = originPoint[i].fY + (midpoints[backi].fY + offsety - originPoint[i].fY) * scale;
        int extranexti = (extraindex + 1) % (2 * originPoint.size());
        extrapoints[extranexti].fX = originPoint[i].fX + (midpoints[i].fX + offsetx - originPoint[i].fX) * scale;
        extrapoints[extranexti].fY = originPoint[i].fY + (midpoints[i].fY + offsety - originPoint[i].fY) * scale;
    }
}
 
void createBezierCurve(const vector<SkPoint> &originPoint, vector<SkPoint> &curvePoint)
{
    vector<SkPoint> extrapoints;
    createCurve(originPoint, extrapoints);
 
    SkPoint controlPoint[4];
    //生成4控制点，产生贝塞尔曲线
    for(int i = 0 ; i < originPoint.size() ; i++)
    {
        controlPoint[0] = originPoint[i];
        int extraindex = 2 * i;
        controlPoint[1] = extrapoints[extraindex + 1];
        int extranexti = (extraindex + 2) % (2 * originPoint.size());
        controlPoint[2] = extrapoints[extranexti];
        int nexti = (i + 1) % originPoint.size();
        controlPoint[3] = originPoint[nexti];
        SkScalar u = 1;
        while(u >= 0)
        {
            SkScalar px = bezier3funcX(u, controlPoint);
            SkScalar py = bezier3funcY(u, controlPoint);
            //u的步长决定曲线的疏密
            u -= 0.005;
            SkPoint tempP;
            tempP.fX = px;
            tempP.fY = py;
            //存入曲线点
            curvePoint.push_back(tempP);
        }
    }
}
 
//三次贝塞尔曲线
SkScalar bezier3funcX(SkScalar uu, SkPoint *controlP)
{
    SkScalar part0 = controlP[0].fX * uu * uu * uu;
    SkScalar part1 = 3 * controlP[1].fX * uu * uu * (1 - uu);
    SkScalar part2 = 3 * controlP[2].fX * uu * (1 - uu) * (1 - uu);
    SkScalar part3 = controlP[3].fX * (1 - uu) * (1 - uu) * (1 - uu);
    return part0 + part1 + part2 + part3;
}
 
SkScalar bezier3funcY(SkScalar uu, SkPoint *controlP)
{
    SkScalar part0 = controlP[0].fY * uu * uu * uu;
    SkScalar part1 = 3 * controlP[1].fY * uu * uu * (1 - uu);
    SkScalar part2 = 3 * controlP[2].fY * uu * (1 - uu) * (1 - uu);
    SkScalar part3 = controlP[3].fY * (1 - uu) * (1 - uu) * (1 - uu);
    return part0 + part1 + part2 + part3;
}

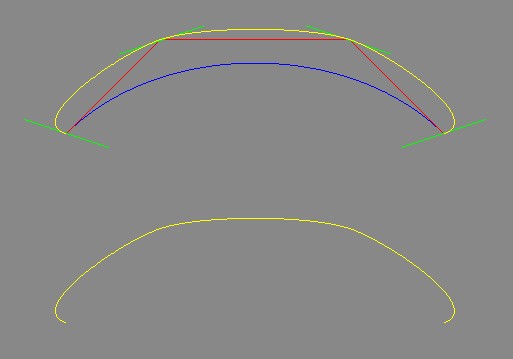
因为skia本身有贝塞尔的相应画法,所以createCurve只用算出新增的两个控制点的坐标即可

而从坐标向下平移50个单位后的贝塞尔曲线可以看出…如果自己通过三次贝塞尔插值createBezierCurve其实画得也不差嘛,哈哈…